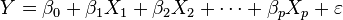REGRESION

Las técnicas de regresión permiten hacer predicciones sobre los valores de cierta variable Y (dependiente), a partir de los de otra X (independiente), entre las que intuimos que existe una relación. Para ilustrarlo retomemos los ejemplos mencionados al principio del capítulo. Si sobre un grupo de personas observamos los valores que toman las variables.

EJEMPLO DE REGRESION

COMENTARIO:
regresion como su nombre lo indica es regresar a estudiar los fenomenos pasados y ver si tienen relacion.

Regresión Lineal

Se conoce como regresión lineal, correlación de Pearson o método de mínimos cuadrados, al procedimiento de encontrar la ecuación de la recta "que mejor se ajuste a un conjunto de puntos". El método de mínimos cuadrados nos permite encontrar el grado de correlación lineal entre un conjunto de pares de valores numéricos. La regresión lineal o ajuste lineal es un método matematico modeliza relación entre una variable dependiente Y, las variables independientes X_i y un término aleatorio ε. Este modelo puede ser expresado como:

donde β₀ es la intersección o término "constante", las β_i son los parámetros respectivos a cada variable independiente, y p es el número de parámetros independientes a tener en cuenta en la regresion. La regresión lineal puede ser contrastada con la regresion no lineal.

COMENTARIO:

Como su nombre lo indica es lineal entonces cuando la grafiquemos los puntos deben estar en una parte donde se pueda trazar una linea recta ya que todos los fenomenos deben estar serca de ella.

cuando la regresion es positiva los puntos deben de estar hacia arriba, y cuando es negativa los puntos deben de estar hacia abajo.

TERCER BIMESTRE:

• RELACION Y CORRELACION
• SERIES DE TIEMPO
• NUMEROS DE INDICE
• INTRODUCCION A LA PROBABILIDAD

REGRESION Y CORRELACION

Regresión y Correlación

La regresión y la correlación son dos técnicas estrechamente relacionadas y comprenden una forma de estimación.

En forma más especifica el análisis de correlación y regresión comprende el análisis de los datos muestrales para saber que es y como se relacionan entre si dos o mas variables en una población. El análisis de correlación produce un número que resume el grado de la correlación entre dos variables; y el análisis de regresión da lugar a una ecuación matemática que describe dicha relación.

El análisis de correlación generalmente resulta útil para un trabajo de exploración cuando un investigador o analista trata de determinar que variables son potenciales importantes, el interés radica básicamente en la fuerza de la relación. La correlación mide la fuerza de una entre variables; la regresión da lugar a una ecuación que describe dicha relación en términos matemáticos

EJEMPLOS DE REGRESION Y CORRELACION

COMENTARIO:

regresion y correlacion son dos metodos muy distintos ya que regresion estudia los fenomenos del pasdado y correlacion estudia dos fenomenos osea mutuamente y ver si tienen relacion una con otra. pero los dos metodos nos sirven para cualquier investigacion

MINIMOS CUADRADOS

MINIMOS CUADRADOS

Es una técnica de analisis numerico encuadrada dentro de la optimizacion matamatica, en la que, dados un conjunto de pares, se intenta encontrar la funcion mejor se aproxime a los datos (un "mejor ajuste"), de acuerdo con el criterio de mínimo error cuadrático.

En su forma más simple, intenta minimizar la suma de cuadrados de las diferencias ordenadas entre los puntos generados por la función y los correspondientes en los datos. Específicamente, llama minimos cuadrados promedio, cuando el número de datos medidos es 1 y se usa el método de descenso por gradiente para minimizar el residuo cuadrado. Se puede demostrar que LMS minimiza el residuo cuadrado esperado, con el mínimo de operaciones (por iteración), pero requiere un gran número de iteraciones para converger.

Desde un punto de vista estadístico, un requisito implícito para que funcione el método de mínimos cuadrados es que los errores de cada medida estén distribuidos de forma aleatoria. El teorema de Gauss-Markov prueba que los estimadores mínimos cuadráticos carecen de sesgo y que el muestreo de datos no tiene que ajustarse, por ejemplo, a una distribucion normal. También es importante que los datos recogidos estén bien escogidos, para que permitan visibilidad en las variables que han de ser resueltas, para dar más peso a un dato en particular.

La técnica de mínimos cuadrados se usa comúnmente en el ajuste de curvas. Muchos otros problemas de optimización pueden expresarse también en forma de mínimos cuadrados, minimizando la energia o maximizando la entropía.

COMENTARIO:

para que el método de mínimos cuadrados funcione, es que los errores de cada punto estén distribuidos de forma aleatoria. Estos minimos cuadrados se utilizan en el ajuste de curvas y no contienen mucho sesgo, tambian que el muesteo de los datos no se tiene que ajustar.